Tässä artikkelissa kuvataan Base Camp –hankkeen etäteknologiakokeilun vaatimaa jatkokehitystä virtuaalihologrammien visualisointiratkaisuun. Edellisessä artikkelissa käsiteltiin, miten pistepilvelle luodaan staattinen 3D-malli projisointia varten. Tässä artikkelissa johdetaan projektioalgoritmin toteutus matemaattisesti.
Mistä projektiossa on kyse?
2D-kuvapisteen projektioon tarvitaan kuvan koko vaaka- ja pystysuunnassa. Tämän lisäksi on tiedettävä kameran polttoväli. Polttoväli esitetään kulmayksiköinä; tässä artikkelissa sitä käsitellään asteina. Kameran ajatellaan tällöin olevan kuvan keskipisteessä.
Asioiden yksinkertaistamiseksi käsittelemme aluksi vain yhtä leveyssuuntaista projektiota, mutta vastaava toiminnallisuus on toki laajennettavissa myös pystysuuntaan. Kuvapisteen leveyssuuntainen koordinaatti kuvataan etäisyytenä kuvan keskipisteestä suhteellisella arvovälillä [1,-1]. Kuten kuvasta 1 havaitaan, projektiosta löytyy suorakulmainen kolmio, jolloin sivun z pituus on laskettavissa trigonometrista kaavaa hyödyntämällä.
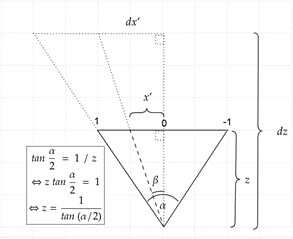
Miten yksittäisen pisteen projisointi toimii?
Yksittäisen pisteen projisointia varten kuvasta on valittava mielivaltainen piste, jonka suhteellinen etäisyys keskipisteestä esitetään symbolilla x’. Pisteen ja z-sivun muodostaman suorakulmaisen toista kolmion kulma esitetään symbolilla β. Tällöin voimme muodostaa kuvassa 2 näkyvät yhtälöt.
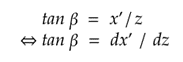
Jos syvyyssuuntaa z kasvatetaan mielivaltaisella arvolla d, myös arvon x’ täytyy kasvaa samassa suhteessa, jotta kolmion kulma pysyy samana. Tästä voimme päätellä, että jos sivun z pituus on yksi, saamme laskettua syvyysarvon perusteella leveyssuuntaisen etäisyyden keskipisteestä kertomalla suhteellisen etäisyyden arvolla d. Näppärää!
Koska kuvassa 1 näkyvä arvo z ei ole aina pituudeltaan välttämättä yksi, meidän on muokattava se sellaiseksi. Olkoon olemassa S, joka kerrottuna sivun z pituudella antaa arvon yksi. Koska jo aiemmin esitettiin z:n arvo riippuvaksi kulmasta α, voimme ratkaista S:n yhtälöstä kuvassa 3 esitetyllä tavalla.
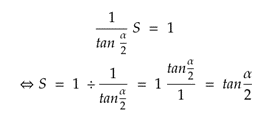
Tämän avulla saamme uudet suhteelliset etäisyydet keskipisteestä vaakasuuntaisille kuvapisteille, kuten kuvassa 4 on havainnollistettu. Sivun z pituudeksi muodostuu aina yksi. Koska vaakasuuntaiset minimi- ja maksimiarvot kuvassa 1 olivat välillä [1, 1], voimme sijoittaa S:n suoraan reunapisteisiin. Pystysuuntainen etäisyys saadaan laskettua täysin samalla menetelmällä, mutta α:n paikalla käytetään pystysuuntaista kulmaa.
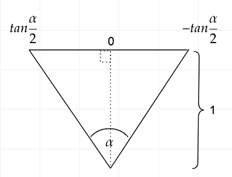
Miten tästä luodaan algoritmi?
Asioiden esittämisen helpottamiseksi koodista on jätettävä pois mahdolliset kameravääristymien korjaukset. Edellisessä artikkelissa kuvatun projektiopistemallin neliöiden projisointi tapahtuu seuraavasti.
Ensiksi laskemme kuvapisteen suhteellisen sijainnin kameran keskipisteestä. Syvyyskameran toteutuksesta johtuen oikea keskipiste ei välttämättä ole kuvan keskipiste. Tämän vuoksi on tiedettävä vielä kameran linssin keskipisteen sijainti kuvassa. Nämä tiedot saamme onneksi selville Intel Realsense SDK:n rajapintafunktioiden avulla rs2_intrinsics-tietorakenteesta.
Vektori kuvapisteenSijainti on pikselin (x,y)-koordinaatti kuvan vasemmasta yläkulmasta katsottuna. Syvyysarvo syvyys näytteistetään tallenteen videotekstuurin korkeuskarttakuvasta. kameransijaintiKuvassa toimii keskipisteenä. Vektori polttoVali sisältääsuhteelliset etäisyyskertoimet x sekä y kerrottuna kuvan leveyden ja korkeuden puolikkailla. Tällöin lopullinen sijainti on laskettavissa suoraan kuvapistekoordinaattien avulla, eikä muunnosta suhteellisiin koordinaatteihin tarvitse välissä tehdä. Listauksessa 1 näkyvä pseudokoodin C++-toteutus on tarkasteltavissa Intel Realsense SDK:n funktiossa rs2_deproject_pixel_to_point.
float3 pisteprojektio( float2 kuvapisteenSijainti, float syvyys,
float2 kameransijaintiKuvassa, float2 polttoVali)
{
float x = (kuvapisteenSijainti.x – kameransijaintiKuvassa.x) / polttoVali.x;
float y = (kuvapisteenSijainti.y – kameransijaintiKuvassa.y) / polttoVali.y;
return float3(syvyys* x, syvyys* y, syvyys);
}
Listaus 1. Pistepilven projektioalgoritmi pseudokoodina.
Virtuaalihologrammeja varten listauksen pseudokoodi toteutettiin Unity-sovelluskehittimen GLSL-verteksivarjostinohjelmana, joka suoritetaan kaikille projektiopistemallin neliöiden vertekseille. Kameran sijaintitieto sekä polttoväli oli helpoin välittää uniform-tyyppisinä vain-luku-muuttujina editorista käsin nelikomponenttivektorissa. Kuvapistekohtainen syvyystieto on näytteistettävissä videotekstuurin korkeuskarttaa kuvaavasta osiosta.
Syvyyskartan ja kameran värikuvan kokoerojen vuoksi varjostinohjelmaan toteutettiin myös koordinaattien sovitus kuvien kesken, jolloin samat suhteelliset koordinaatit toimivat molemmille kuvatyypeille. Toteutuksen tarkempi läpikäynti jätetään toistaiseksi väliin sen varsin teknisen luonteen vuoksi.
Yhteenveto
Tässä artikkelissa on kuvattu pistepilviprojektion tekemisen sekä siitä algoritmin johtamisen matemaattinen tausta. Seuraavassa artikkelissa käsitellään menetelmiä pistepilven yhtenäistämiseen sekä lopputulosta selkeästi heikentävien kohtien poisrajaamiseen.
Kirjoittaja:
Anssi Gröhn, lehtori, Karelia-ammattikorkeakoulua
Base Camp -Opiskelijayrittäjyysalustojen kehittäminen -hanke
Artikkelikuva: Richard Horvath on Unsplash

