Karelia-ammattikorkeakoulun energia- ja ympäristö-, talo- ja rakennustekniikan ensimmäisen vuoden pakollisiin opintoihin kuuluu differentiaali- ja integraalilaskennan opintojakso. Opintojaksolla osaaminen osoitetaan välikokeilla sekä palautetuilla laskuharjoitustehtävillä. Kevään arviointia tehdessä huomio kiinnittyi siihen, että hyvän arvosanan saaneet olivat tyypillisesti palauttaneet tehtäviä hyvin, kun taas monilta hylätyn arvosanan saaneilta tehtävät olivat jäänet joko täysin tai lähes kokonaan palauttamatta. Olisiko tehtyjen laskuharjoitustehtävien ja kurssin arvosanan välillä todellista riippuvuutta?
Selvitimme energia- ja ympäristö-, talo- ja rakennustekniikan ensimmäisen vuoden ryhmien menestystä differentiaali- ja integraalilaskennan opintojaksolla (n=94). Lisäksi selvitimme tehtyjen laskuharjoitustehtävien tekemisen merkitystä kurssilla menestymiseen.
Laskuharjoitustehtävien tekeminen jaettiin kolmeen kategoriaan, sen mukaan kuinka paljon laskuharjoitustehtäviä on laskettu: alle 50 %, 50 %-85 % ja yli 85 %. Kurssiarvosanojen sijaan käytimme laadullisia määreitä hylätty (arvosana 0), tyydyttävä (arvosanat 1 ja 2), hyvä (arvosanat 3 ja 4) ja kiitettävä (arvosana 5).
Tulosten käsittely
Tutkimme kurssimenestyksen ja tehtyjen laskuharjoitustehtävien riippuvuutta 2– riippumattomuustestillä. Testin nollahypoteesi H0 = opinnoissa menestyminen ei riipu laskuharjoitustehtävien tekemisestä ja työhypoteesi H1 = opinnoissa menestymien riippuu laskuharjoitustehtävien tekemisestä. Kuten kuvasta 1 nähdään opintomenestyksen jakaumat ovat varsin erilaiset tehtyjen laskuharjoitustehtävien suhteen. Näyttäisi, että mitä enemmän opiskelija on tehnyt laskuharjoitustehtäviä, niin sitä paremmin hän on menestynyt opinnoissa.
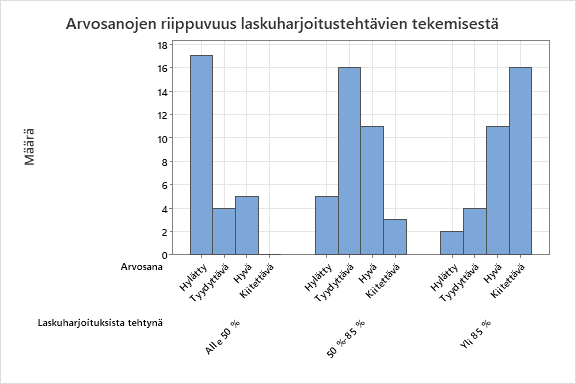
2– riippumattomuustestin perusteella opintomenestys riippuu tilastollisesti erittäin merkitsevästi (p-arvo <0,001) laskuharjoitustehtävien tekemistä. Alle 50 % laskuharjoitustehtävistä tekevistä opiskelijoista jopa 65 % sai hylätyn opintojaksosta ja kiitettävää ei saanut yksinään tähän kategoriaan kuuluvista opiskelijoista. Yli 85 % laskuharjoitustehtävistä suorittaneista lähes puolet saivat kiitettävän suorituksen opintojaksosta. Hylätyn yli 85 % laskuharjoitustehtävistä laskeneista sai ainoastaan 2 opiskelijaa. Analyysin perusteella on kiistatta selvää, että laskuharjoitusten tekeminen parantaa merkittävästi opintosuoritusta. (p-arvo<0,001, df=6,
2=53,57)
| Alle 50 % | 50 %-85 % | Yli 85 % | Kaikki | |
| Hylätty | 65,38 | 14,29 | 6,06 | 25,53 |
| Tyydyttävä | 15,38 | 45,71 | 12,12 | 25,53 |
| Hyvä | 19,23 | 31,43 | 33,33 | 28,72 |
| Kiitettävä | 0,00 | 8,57 | 48,48 | 20,21 |
| Kaikki | 100,00 | 100,00 | 100,00 | 100,00 |
Harjoitustehtävien tekeminen kannattaa
Tämä tulos osoittaa selkeästi laskuharjoitustehtävien tekemisen tärkeyden. Tulevaisuudessa matematiikan kurssien alussa ei voi liikaa kannustaa harjoitustehtävien tekemiseen. Toistot lisäävät laskurutiinia ja sitä kautta ymmärrystä, mikä parantaa suoriutumista vaativammissakin tehtävissä. Toivottavasti laskurutiinin ja ymmärryksen lisääntyminen edistää suoriutumista matemaattisista haasteista muissakin opiskeltavissa aineissa.
Kirjoittajat:
Jani Kangas, lehtori, Karelia-ammattikorkeakoulu
Lisbeth Smolander, lehtori, Karelia-ammattikorkeakoulu

